Безталанова И.Г.
Тип урока. Решение частной задачи.
Оборудование: планы урока, составленные детьми, листы для групповой работы, на одном из которых начерчен равнобедренный треугольник, на другом — равносторонний, на третьем — разносторонний, маркеры (по количеству групп).
Ход урока
I. Создание ситуации успеха.
(На доске вывешены все планы урока, составленные детьми. Одной из задач урока, проведенного накануне, было обсуждение детских планов. Ребята пришли к выводу, что наиболее точные планы составлены Яной и Викой)
У.: Сегодняшний урок пройдет по составленному вами плану. Благодаря вам мне было легко готовиться к уроку. Чему будет посвящен урок?
Д.: Площади.
У: Какие вопросы вы можете задать друг другу по этой теме?
Д.: Что такое площадь?
Чем площадь отличается от периметра?
Бывают ли фигуры, у которых нет площади?
Какие это фигуры?
Есть ли такие фигуры, у которых есть периметр, но нет площади, и наоборот?
Как найти площадь прямоугольника? Как найти площадь прямоугольного треугольника?
На доске запись:
1) x = а • Ь 3) х = а - b : 2 5) х = 93 – З а – 2 b - с – 6 d
2) х = 2а + 2b 4) х =18:3
У: Определите, чем является х в каждом случае. Не записывая формулу, поставьте ее номер, схематично изобразите фигуру и обозначьте то, что в ней находят, т. е. искомую величину.
(Далее проводится фронтальная проверка выполнения задания.)
Влад: (рассказывающий о формуле №1): В данном случае х — это площадь прямоугольника. (Дети соглашаются.)
Настя: (работающий с формулой №2): В данном случае х — это периметр прямоугольника.
Д.: И все?
Р. (задумывается): Еще это может быть периметр параллелограмма.
Д.: И все?
Настя: А, поняла, еще ромбоида.
(Дети соглашаются.)
Саша: (работающий с формулой №3): В данном случае находят площадь прямоугольного треугольника.
(Дети соглашаются.)
Аня: (работающая с формулой №4): Я думаю, что здесь х — это сторона равностороннего треугольника.
Д.: Почему?
Аня: Потому что мы периметр делим на три одинаковых части, а это возможно только у равностороннего треугольника.
Д.: А больше ничем х не может быть?
Аня: Может быть, и может, но я не знаю.
Д.: Думаю, х может быть одной из сторон прямоугольника, если 18 — это площадь, а 3 — это другая сторона.
(Дети соглашаются.)
Никита: (работающий с формулой №5): В данном случае х — это сторона многоугольника.
Д.: А сколько у него углов?
Никита: Сейчас посчитаю. (Считает вслух.) Три и два — это пять. Сторона с одна — это шесть. И еще шесть — это двенадцать. Значит, мы ищем тринадцатую сторону, х — это сторона тринадцатиугольника.
(Дети соглашаются.)
У: Молодцы! Поднимите руки те, для кого это задание было легким.
(Практически все дети поднимают руки.)
У: Думаю, что и следующее задание будет для вас интересным. Начертите у себя в тетради одну фигуру, запишите формулу и вычислите ее площадь. (Взаимопроверка.)
У: Поднимите руку те, чей сосед справился с заданием без ошибок.
Учитель обращается поочередно к нескольким детям с вопросом: «По какой формуле ты находил(а) площадь своей фигуры?»
(После того как ребенок прочитывает формулу, дети определяют, какая фигура начерчена у него в тетради.)
II. Постановка и решение частной задачи.
У: Мы можем переходить к следующему пункту нашего плана?
Д.: Можем.
У: Что мы собирались делать дальше?
Д.: Нужно выбрать фигуру, площадь которой мы будем сегодня находить.
У: Я знаю, что вам хотелось находить площадь «сложной» фигуры, но если не возражаете, то я предлагаю начать с треугольника. (Дети соглашаются.)
У: Какие вы знаете треугольники?
Д.: Равнобедренный, равносторонний, разносторонний.
У: Будем работать отдельно с каждым или сразу со всеми, поскольку они треугольники? Д.: Сразу со всеми.
У.: Как будете работать?
Д.: Конечно, в группах. У нас так и в плане написано.
По просьбе учителя дети собираются в три группы. Учитель дает первой группе большой лист с начерченным равнобедренным треугольником; второй группе — лист с начерченным равносторонним треугольником; третьей группе — лист с начерченным разносторонним треугольником.
У (обращается к группам): Что будете искать?
Д.: Площадь треугольника.
У: Что вам в этом поможет?
Д.: Прямоугольник и прямоугольный треугольник.
У: Найдите рациональный способ и зафиксируйте его в удобной форме.
Работа в группах
Обсуждение результатов работы групп.
Результаты работы групп выглядели таким образом:
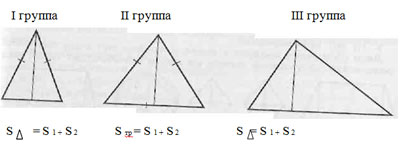
У: Что вы можете сказать о способах, найденных группами?
Д.: Это один и тот же способ.
У: В чем он заключается?
Д.: Внутри треугольника нужно провести отрезок так, чтобы треугольник превратился в два прямоугольных треугольника. Нужно найти сначала площадь первого прямоугольного треугольника, затем второго и эти площади сложить.
Андрей: А я увидел ещё один способ нахождения площади непрямоугольного треугольника.
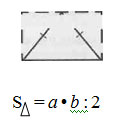
У.: В таком случае следует обсудить, какой из способов рациональнее.)
У.: Как могло получиться, что для нахождения площади разных треугольников вы использовали один и тот же способ?
Д.: Какая разница, какой треугольник разбивать на прямоугольные треугольники? Я думаю, что и с другими фигурами надо так поступать.
У. (соглашается и показывает): Этот отрезок, выходящий из вершины угла и опускающийся на противоположную сторону под прямым углом, называется высотой. Высота обозначается буквой h. Запишите способ в тетрадь.
У.: У вас появилась замечательная мысль относительно нахождения площади других фигур. Хотите ее проверить?
Д.: Хотим.
Учитель открывает запись на доске:
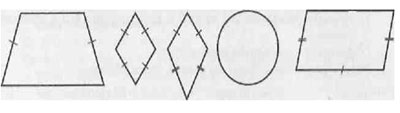
У: Ну что, есть варианты?
Дети по одному выходят к доске и предлагают свои варианты. В результате обсуждения запись на доске приобретает такой вид:
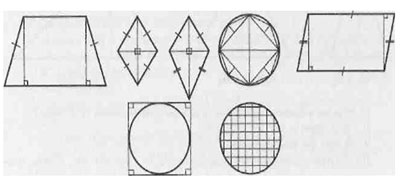
III. Итоговая рефлексия.
У: Урок подходит к концу. Что еще осталось в нашем плане?
Д.: Нужно записать способы формулами.
Еще нужно выяснить, может быть, другие способы есть.
Нужно научиться пользоваться способами.
Нет, сейчас мы не успеем все это сделать. Нужно подвести итог урока.
У: Хорошо. Кто хочет это сделать?
Д.: Какую цель мы поставили на прошлом уроке?
Как бы вы назвали наш урок?
Нашли способ?
В чем он заключается?
Что было на уроке самым важным?
Что будем делать завтра?
Кто хочет кого-нибудь похвалить?
К концу учебного года обучения учитель фактически передает функцию планирования продвижения в освоении предметного содержания коллективному субъекту учебной деятельности.


